BAB I
PENDAHULUAN
A.
LATAR BELAKANG
Media masa (pers) sesungguhnya adalah media informasi yang bersifat
netral di tangan masyarakat. Media massa menyampaikan informasi dengan didukung
fakta yang kuat sehingga diharapkan tidak ada keberpihakan di dalamnya. Namun
demikian, media massa tidak selalu obyektif dalam menjalankan fungsinya. Terkadang
media massa selalu berorientasi bisnis, sehingga perhitungan yang dipakai
adalah keuntungan materi semata. Ketika mempublikasikan berita dan foto
misalnya, nilai-nila etika kurang diperhatikan, yang penting secara materi
media tersebut bisa memperoleh keuntungan.
Dalam pengelolaan pers, sesungguhnya
ada aturan main yang menjadi acuan bagi setiap wartawan, yaitu lewat kode etik
jurnalistik. Pedoman yang dimuat dalam kode etik jurnalistik secara umum adalah
member arahan kepada wartawan agar senantiasa memperhatikan nilai-nilai etika
dalam menjalankan profesi kewartawanan. Dalam menulis berita misalnya, wartawan
dituntut harus menulis berita dengan jujur dan tanpa ada rekayasa, obyektif dan
didukung dengan fakta yang kuat. Dengan demikian diharapkan jangan sampai
wartawan menulis berita bohong atau fitnah yang bisa berakibat fatal bagi yang
diberitakan.
Berita yang disajikan oleh media
massa dengan sendirinya akan menimbulkan opini yang berfariasi ditengah
masyarakat. Karena setiap berita yang muncul di media menurut William Rivers, bisa
dipersepsi secara berbeda oleh maasyarakat. Untuk itu agar opini masyarakat
tidak salah persepsi pada sebuah pemberitaan, maka kata kuncinya perlu
kejujuran bagi setiap wartawan dalam menyajikan berita.
Media massa mempunyai peranan yang
sangat penting dalam menyebarkan berbagai informasi ditengah masyarakat. Berita
yang dipublikasikan lewat media massa, baik yang positif maupun yang negatif
akan begitu cepat diketahui oleh masyarakat luas, sehingga dapat mempengaruhi
cara pikir masyarakat. Manakala informasi yang diberikan itu jujur dan obyektif
maka akan sangatpositif hasilnya bagi masyarakat.sebaliknya manakala informasi
yang diberikan itu bohong dan subjektif, maka akan berakibat negatife bahkan
dapat menimbulkan konflik di tengah masyarakat.Itulah mengapa menurut Jhon
Hohenberg, bahwa berita di media massa harus selalu memperhatikan aktualitas, kejujuran
dan pendidikan. Dalam mengemban tugas tersebut maka tidak berlebihan kalau
media massa memiliki tugas luhur yang ikut andil dalam usaha mencerdaskan
kehidupan bangsa.
B. Rumusan
Masalah
1.
Bagaimana manfaat pers dalam kehidupan sehari-hari ?
2.
Bagaimana dampak penyalahgunaan kebebasan pers ?
3.
Bagaimana dampak kebebasan pers terhadap individu,masyarakat,dan Negara?
4.
Bagaimana Pasal-pasal yang mengatur tentang tindak penyalahgunaan kebebasan pers ?
C. Tujuan
1.
Menjelaskan
manfaat pers dalam kehidupan sehari- hari.
2.
Menjelaskan
dampak
penyalahgunaan kebebasan pers.
3.
Menjelaskan
dampak kebebasan pers terhadap individu, masyarakat, dan negara.
4.
Menjelaskan
yang mengatur penyalahgunaan kebebasan pers.
Posted by : Unknown on : With
0komentar



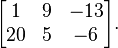
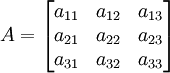



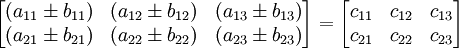
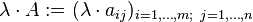


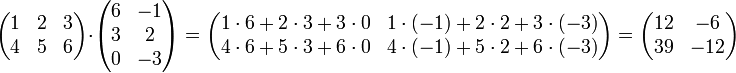


 bukanlah persamaan linear.
bukanlah persamaan linear. ,
,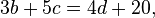 ,
,








