2013

buat tugas makalah

Diposting oleh Unknown | Senin, 25 November 2013

buat tugas makalah

Posted by : Unknown on :Senin, 25 November 2013 With 0komentar

link temen"

Diposting oleh Unknown | Senin, 28 Oktober 2013

bahasa inggris
additn.blogspot.com
zahrakhomar.blogspot.com
ceritayazin.blogspot.com
sabtarieka.blogspot.com
riskhilathifah.blogspot.com
rizha.29.blogspot.com
vickywulan.blogspot.com
bahasa indonesia
lofitasari23.blogspot.com
kikiputrasangpemimpi.blogspot.com
lufitanisa.blogspot.com
palupi98.blogspot.com
lillarozzyasih.blogspot.com
biologi
fatmatri.blogspot.com
kangmasman.blogspot.com
gigihsuryanto13.blogspot.com
rohmaindah.blogspot.com
fatimahbiologi.blogspot.com
fisika
dianarist.blogspot.com
elinadwi.blogspot.com
ayukusuma8.blogspot.com
endanwa.blogspot.com
kimia
pejantantangguh20.blogspot.com
arinimila.blogspot.com
aisahnoer.blogspot.com
andrechoiru.blogspot.com
desitaevasilawana05.blogspot.com
shinseogondang.blogspot.com
matematika
khoirotunnisak019.blogspot.com
khodiyah.blogspot.com
khusnul1903.blogspot.com
irahefpytanawaworuntu.blogspot.com

link temen"

Posted by : Unknown on :Senin, 28 Oktober 2013 With 0komentar

matriks

Diposting oleh Unknown | Senin, 07 Oktober 2013

Baca selengkapnya »

Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu

$\begin{bmatrix}1 & 9 & -13 \\20 & 5 & -6 \end{bmatrix}.$

Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi.
Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.
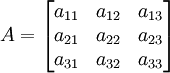
$A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \!$

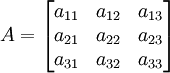
Notasi

Matriks pada umumnya ditulis dalam tanda kurung siku/kurung tegak:

$\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}.$

Operasi dasar

Penjumlahan dan pengurangan matriks

Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.

$a_{ij} \pm b_{ij} = c_{ij}\!$

atau dalam representasi dekoratfinya

$\begin{bmatrix} {3} & {4} \\ {6} & {5} \\ \end{bmatrix} \!$

$\begin{bmatrix} (a_{11} \pm b_{11}) & (a_{12} \pm b_{12}) & (a_{13} \pm b_{13}) \\ (a_{21} \pm b_{21}) & (a_{22} \pm b_{22}) & (a_{23} \pm b_{23}) \\ \end{bmatrix} = \begin{bmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ \end{bmatrix} \!$

Perkalian skalar

Matriks dapat dikalikan dengan sebuah skalar.

$\lambda\cdot A := (\lambda\cdot a_{ij})_{i=1, \ldots , m; \ j=1, \ldots , n}$

Contoh perhitungan :

$5 \cdot \begin{pmatrix} 1 & -3 & 2 \\ 1 & 2 & 7 \end{pmatrix} = \begin{pmatrix} 5 \cdot 1 & 5 \cdot (-3) & 5 \cdot 2 \\ 5 \cdot 1 & 5 \cdot 2 & 5 \cdot 7 \end{pmatrix} = \begin{pmatrix} 5 & -15 & 10 \\ 5 & 10 & 35 \end{pmatrix}$

Perkalian Matriks

Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.

$c_{ij}=\sum_{k=1}^m a_{ik}\cdot b_{kj}$

Contoh perhitungan :

$\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \cdot \begin{pmatrix} 6 & -1 \\ 3 & 2 \\ 0 & -3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 6 + 2 \cdot 3 + 3 \cdot 0 & 1 \cdot (-1) + 2 \cdot 2 + 3 \cdot (-3) \\ 4 \cdot 6 + 5 \cdot 3 + 6 \cdot 0 & 4 \cdot (-1) + 5 \cdot 2 + 6 \cdot (-3) \\ \end{pmatrix} = \begin{pmatrix} 12 & -6 \\ 39 & -12 \end{pmatrix}$

matriks

Posted by : Unknown on :Senin, 07 Oktober 2013 With 0komentar

persamaan linier

Diposting oleh Unknown |

Baca selengkapnya »

Persamaan linear adalah sebuah persamaan aljabar, yang tiap sukunya mengandung konstanta, atau perkalian konstanta dengan variabel tunggal. Persamaan ini dikatakan linear sebab hubungan matematis ini dapat digambarkan sebagai garis lurus dalam Sistem koordinat Kartesius.

Contoh grafik dari suatu persamaan linear dengan nilai m=0,5 dan b=2 (garis merah)

Bentuk umum untuk persamaan linear adalah

$y = mx + b.\,$

Dalam hal ini, konstanta m akan menggambarkan gradien garis, dan konstanta b merupakan titik potong garis dengan sumbu-y. Persamaan lain, seperti x³, y^1/2, dan $xy$ bukanlah persamaan linear.

Contoh

Contoh sistem persamaan linear dua variabel:

$x + 2y = 10,\,$ ,

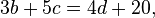$3b + 5c = 4d+ 20,\,$ ,

$5x - 3y +6 = -9x + 8y+ 4,\,$

Sistem Persamaan Linear Dua Variabel

Persamaan linear yang rumit, seperti di sebut di atas, bisa ditulis dengan menggunakan hukum aljabar agar menjadi bentuk yang lebih sederhana. Seperti contoh, huruf besar di persamaan merupakan konstanta, dan x dan y adalah variabelnya.

Bentuk Umum

$Ax + By + C = 0,\,$

dimana konstanta A dan B bila dijumlahkan, hasilnya bukan angka nol. Konstanta dituliskan sebagai A ≥ 0, seperti yang telah disepakati ahli matematika bahwa konstanta tidak boleh sama dengan nol. Grafik persamaan ini bila digambarkan, akan menghasilkan sebuah garis lurus dan setiap garis dituliskan dalam sebuah persamaan seperti yang tertera diatas. Bila A ≥ 0, dan x sebagai titik potong, maka titik koordinat-xadalah ketika garis bersilangan dengan sumbu-x (y = 0) yang digambarkan dengan rumus -c/a. Bila B≥ 0, dan y sebagai titik potong, maka titik koordinat- y adalah ketika garis bersilangan dengan sumbu-y (x = 0), yang digambarkan dengan rumus -c/b.

Bentuk standar

$ax + by = c,\,$

di mana, a dan b jika dijumlahkan, tidak menghasilkan angka nol dan a bukanlah angka negatif. Bentuk standar ini dapat diubah ke bentuk umum, tapi tidak bisa diubah ke semua bentuk, apabila a dan b adalah nol.

Bentuk titik potong gradien

Sumbu-y

$y = mx + b,\,$

dimana m merupakan gradien dari garis persamaan, dan titik koordinat y adalah persilangan dari sumbu-y. Ini dapat digambarkan dengan x = 0, yang memberikan nilai y = b. Persamaan ini digunakan untuk mencari sumbu-y, dimana telah diketahui nilai dari x. Y dalam rumus tersebut merupakan koordinat y yang anda taruh di grafik. Sedangkan X merupakan koordinat x yang anda taruh di grafik.

Sumbu-x

$x = \frac{y}{m} + c,\,$

dimana m merupakan gradien dari garis persamaan, dan c adalah titik potong-x, dan titik koordinat x adalah persilangan dari sumbu-x. Ini dapat digambarkan dengan y = 0, yang memberikan nilai x = c. Bentuk y/m dalam persamaan sendiri berarti bahwa membalikkan gradien dan mengalikannya dengan y. Persamaan ini tidak mencari titik koordinat x, dimana nilai y sudah diberikan.

ء-

Sistem persamaan linear lebih dari dua variabel

Sebuah persamaan linear bisa mempunyai lebih dari dua variabel, seperti berikut ini:

$a_1 x_1 + a_2 x_2 + \cdots + a_n x_n = b.$

di mana dalam bentuk ini, digambarkan bahwa a₁ adalah koefisien untuk variabel pertama, x₁, dan n merupakan jumlah variabel total, serta b adalah konstanta.

persamaan linier

Posted by : Unknown on : With 0komentar

Trigonometri

Diposting oleh Unknown | Jumat, 04 Oktober 2013

Baca selengkapnya »

Trigonometri

Posted by : Unknown on :Jumat, 04 Oktober 2013 With 0komentar

Baca selengkapnya »

Rumus: Logika matematika - materi SMA Kelas X

Diposting oleh Unknown |

Baca selengkapnya »

Rumus: Logika matematika - materi SMA Kelas X LOGIKA MATEMATIKA A. Pernyataan Yang dimaksud dengan kalimat atau pernyataan adalah kalimat yang mempunyai nilai benar atau salah, tetapi tidak sekaligus benar dan salah. Ada dua jenis kalimat matematika, yaitu : Kalimat tertutup, merupakan pernyataan yang nilai kebenarannya sudah pasti. Contoh : a) 3 x 4 = 12 (pernyataan tertutup yang benar) b) 3 + 4 = 12 (pernyataan tertutup yang salah) Kalimat terbuka, merupakan pernyataan yang kebenarannya belum pasti. Contoh : a : Ada daun yang berwarna hijau b : Gula putih rasanya manis B. Ingkaran Pernyataan Ingkaran atau negasi suatu pernyataan adalah pernyataan yang menyangkal pernyataan yang diberikan. Ingkaran suatu pernyataan dapat dibentuk dengan menambah “Tidak benar bahwa ...” di depan pernyataan yang diingkar. Ingkaran pernyataan adalah ~ p. Contoh : Misalkan pernyataan p : Tembakau yang mengandung nikotin. Ingkaran penyataan p adalah ~ p. Tidak benar bahwa tembakau mengandung nikotin. Tabel kebenaran dari ingkaran C. Pernyataan Majemuk (i) Konjungsi Pernyataan p dengan q dapat digabung dengan kata hubung logika “dan” sehingga membentuk pernyataan majemuk “p dan q” yang disebut konjungsi. Konjungsi “p dan q” dilambangkan dengan (ii) Disjungsi Pernyataan p dengan q dapat digabung dengan kata hubung logika “atau” sehingga membentuk pernyataan majemuk “p atau q” yang disebut disjungsi. Disjungsi p atau q dilambangkan dengan . (iii) Implikasi Implikasi “jika p maka q” dilambangkan dengan . (iv) Biimplikasi Biimplikasi “p jika dan hanya jika q” dilambangkan dengan . D. Ekuivalensi Pernyataan – Pernyataan Majemuk E. Konvers, Invers, dan Kontraposisi Dari sebuah implikasi dapat diturunkan pernyataan yang disebut konvers, invers dan kontraposisi dari implikasi tersebut. Tetap semangat ya belajarnya... =)

Rumus: Logika matematika - materi SMA Kelas X

Posted by : Unknown on : With 0komentar

soal-soal

Diposting oleh Unknown | Jumat, 27 September 2013

Baca selengkapnya »

soal-soal

Posted by : Unknown on :Jumat, 27 September 2013 With 0komentar

materi matematika

Diposting oleh Unknown |

Baca selengkapnya »

materi matematika

Posted by : Unknown on : With 0komentar

intergal

Diposting oleh Unknown | Senin, 23 September 2013

Baca selengkapnya »

Integral Tak Tentu

Integral tak tentu mempunyai rumus umum:
$\int F(x) dx = F(x) + c$
Keterangan:

c : konstanta

Pengintegralan standar

Jika $f(x) = a$ maka:
$\int a \operatorname{d}x = ax + c$
Jika $f(x) = ax^n$ maka:
$\int ax^n \operatorname{d}x = (\frac {ax^{n+1}} {n+1}) + c$
Jika $f(x) = (ax + b)^n$ maka:
$\int (ax+b)^n \operatorname{d}x = (\frac {(ax+b)^{n+1}} {a(n+1)}) + c$

Pengintegralan khusus

$\int \frac 1 x\ dx = \ln|x| + k$
$\int \frac {f'(x)} {f(x)} dx = \ln f(x)+ k$
$\int \frac 1 x\ dx = \ln|x| + k$

Sifat-sifat

$\int a f(x) \operatorname{d}x = a \int f(x) \operatorname{d}x + k$

$\int (f(x) \pm g(x)) \operatorname{d}x = \int f(x) \operatorname{d}x \pm \int g(x) \operatorname{d}x$

Integral Tentu

Integral tentu digunakan untuk mengintegralkan suatu fungsi f(x) tertentu yang memiliki batas atas dan batas bawah. Integral tentu mempunyai rumus umum:
$\int_a^b F(x) dx = F(b) - F(a)$
Keterangan:

konstanta c tidak lagi dituliskan dalam integral tentu.

Integral trigonometri

$\int \sin(ax) \ dx = - \frac 1 a \ \cos(ax) + k$
$\int \cos(ax) \ dx = \frac 1 a \ \sin(ax) + k$
$\int \sec(ax) \ tan(ax) \ dx = \frac 1 a \ \sec(ax) + k$
$\int \sec^2(ax) \ dx = \frac 1 a \ \tan(ax) + k$
$\int \csc^2(ax) dx = - \frac {1} {a}\ \cot(ax) + k$
$\int \csc(ax) \ \cot(ax) dx = -\frac {1} {a} \ \csc(ax) + k$

$\int \cos(ax+b) dx = \frac {1}{a} \ \sin(ax+b) + k$
$\int \sin(ax+b) dx = -\frac {1}{a} \ \cos(ax+b) + k$
$\int \sec^2(ax+b) dx = \frac {1}{a} \ \tan(ax+b) + k$

$\int \sec(x) dx = \ln \left\vert \sec(x) + tan(x) \right\vert + k$
$\int \csc(x) dx = -\ln \left\vert \csc(x) + cot(x) \right\vert + k$

$\int \tan(x) dx = -\ln \left\vert \cos(x) \right\vert + k$
$\int \tan(x) dx = \ln \left\vert \sec(x) \right\vert + k$

$\int \cot(x) dx = \ln \left\vert \sin(x) \right\vert + k$
$\int \cot(x) dx = -\ln \left\vert \csc(x) \right\vert + k$

Ingat-ingat juga beberapa sifat-sifat trigonometri, karena mungkin akan digunakan:

$\sin^2 A + \cos^2 A = 1 \,$

$1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,$

$1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,$

$\sin 2A = 2 \sin A \cos A \,$

$\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,$

$2 \sin A \times \cos B = \sin (A + B) + \sin (A - B),$

$2 \cos A \times \sin B = \sin (A + B) - \sin (A - B),$

$2 \cos A \times \cos B = \cos (A + B) + \cos (A - B),$

$2 \sin A \times \sin B = - \sin (A + B) + \cos (A - B),$

Substitusi trigonometri

Integral yang mengandung a² − x²

Pada integral

$\int\frac{dx}{\sqrt{a^2-x^2}}$

kita dapat menggunakan

$x=a\sin(\theta),\quad dx=a\cos(\theta)\,d\theta, \quad \theta=\arcsin\left(\frac{x}{a}\right)$

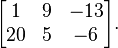
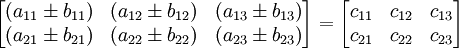
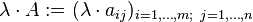
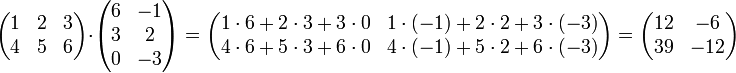
$\begin{align} \int\frac{dx}{\sqrt{a^2-x^2}} & = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2-a^2\sin^2(\theta)}} = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2(1-\sin^2(\theta))}} \\[8pt] & = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2\cos^2(\theta)}} = \int d\theta=\theta+C=\arcsin\left(\frac{x}{a}\right)+C \end{align}$

Catatan: semua langkah diatas haruslah memenuhi syarat a > 0 dan cos(θ) > 0;

Integral yang mengandung a² + x²

Pada integral

$\int\frac{dx}{{a^2+x^2}}$

kita dapat menuliskan

$x=a\tan(\theta),\quad dx=a\sec^2(\theta)\,d\theta$

$\theta=\arctan\left(\frac{x}{a}\right)$

maka integralnya menjadi

$\begin{align} & {} \qquad \int\frac{dx}{{a^2+x^2}} = \int\frac{a\sec^2(\theta)\,d\theta}{{a^2+a^2\tan^2(\theta)}} = \int\frac{a\sec^2(\theta)\,d\theta}{{a^2(1+\tan^2(\theta))}} \\[8pt] & {} = \int \frac{a\sec^2(\theta)\,d\theta}{{a^2\sec^2(\theta)}} = \int \frac{d\theta}{a} = \frac{\theta}{a}+C = \frac{1}{a} \arctan \left(\frac{x}{a}\right)+C \end{align}$

(syarat: a ≠ 0).

Integral yang mengandung x² − a²

Pada integral

$\int\sqrt{x^2 - a^2}\,dx$

dapat diselesaikan dengan substitusi:

$x = a \sec(\theta),\quad dx = a \sec(\theta)\tan(\theta)\,d\theta$

$\theta = \arcsec\left(\frac{x}{a}\right)$

$\begin{align} & {} \qquad \int\sqrt{x^2 - a^2}\,dx = \int\sqrt{a^2 \sec^2(\theta) - a^2} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\ & {} = \int\sqrt{a^2 (\sec^2(\theta) - 1)} \cdot a \sec(\theta)\tan(\theta)\,d\theta = \int\sqrt{a^2 \tan^2(\theta)} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\ & {} = \int a^2 \sec(\theta)\tan^2(\theta)\,d\theta = a^2 \int \sec(\theta)\ (\sec^2(\theta) - 1)\,d\theta \\ & {} = a^2 \int (\sec^3(\theta) - \sec(\theta))\,d\theta. \end{align}$