Latest Post

soal-soal

Diposting oleh Unknown | Jumat, 27 September 2013
Baca selengkapnya »

soal-soal

Posted by : Unknown on :Jumat, 27 September 2013 With 0komentar
| 0 komentar

materi matematika

Diposting oleh Unknown |
Baca selengkapnya »

materi matematika

Posted by : Unknown on : With 0komentar
| 0 komentar

intergal

Diposting oleh Unknown | Senin, 23 September 2013
Baca selengkapnya »

Integral Tak Tentu

Integral tak tentu mempunyai rumus umum:
\int F(x) dx = F(x) + c
Keterangan:
  • c : konstanta

Pengintegralan standar

Jika f(x) = a maka:
\int a \operatorname{d}x = ax + c
Jika f(x) = ax^n maka:
\int ax^n \operatorname{d}x = (\frac {ax^{n+1}} {n+1}) + c
Jika f(x) = (ax + b)^n maka:
\int (ax+b)^n \operatorname{d}x = (\frac {(ax+b)^{n+1}} {a(n+1)}) + c

Pengintegralan khusus

\int \frac 1 x\ dx = \ln|x| + k
\int \frac {f'(x)} {f(x)} dx = \ln f(x)+ k
\int \frac 1 x\ dx = \ln|x| + k

Sifat-sifat

  • \int a f(x) \operatorname{d}x = a \int f(x) \operatorname{d}x + k
  • \int (f(x) \pm g(x)) \operatorname{d}x = \int f(x) \operatorname{d}x \pm \int g(x) \operatorname{d}x

Integral Tentu

Integral tentu digunakan untuk mengintegralkan suatu fungsi f(x) tertentu yang memiliki batas atas dan batas bawah. Integral tentu mempunyai rumus umum:
\int_a^b F(x) dx = F(b) - F(a)
Keterangan:
  • konstanta c tidak lagi dituliskan dalam integral tentu.

Integral trigonometri

  • \int \sin(ax) \ dx = - \frac 1 a \ \cos(ax) + k
  • \int \cos(ax) \ dx = \frac 1 a \ \sin(ax) + k
  • \int \sec(ax) \ tan(ax) \ dx = \frac 1 a \ \sec(ax) + k
  • \int \sec^2(ax) \ dx = \frac 1 a \ \tan(ax) + k
  • \int \csc^2(ax) dx = - \frac {1} {a}\ \cot(ax) + k
  • \int \csc(ax) \ \cot(ax) dx = -\frac {1} {a} \ \csc(ax) + k
  • \int \cos(ax+b) dx = \frac {1}{a} \ \sin(ax+b) + k
  • \int \sin(ax+b) dx = -\frac {1}{a} \ \cos(ax+b) + k
  • \int \sec^2(ax+b) dx = \frac {1}{a} \ \tan(ax+b) + k
  • \int \sec(x) dx = \ln \left\vert \sec(x) + tan(x) \right\vert + k
  • \int \csc(x) dx = -\ln \left\vert \csc(x) + cot(x) \right\vert + k
  • \int \tan(x) dx = -\ln \left\vert \cos(x) \right\vert + k
  • \int \tan(x) dx = \ln \left\vert \sec(x) \right\vert + k
  • \int \cot(x) dx = \ln \left\vert \sin(x) \right\vert + k
  • \int \cot(x) dx = -\ln \left\vert \csc(x) \right\vert + k
Ingat-ingat juga beberapa sifat-sifat trigonometri, karena mungkin akan digunakan:
\sin^2 A + \cos^2 A = 1 \,
1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,
1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,
\sin 2A = 2 \sin A \cos A \,
\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,
2 \sin A \times \cos B = \sin (A + B) + \sin (A - B),
2 \cos A \times \sin B = \sin (A + B) - \sin (A - B),
2 \cos A \times \cos B = \cos (A + B) + \cos (A - B),
2 \sin A \times \sin B = - \sin (A + B) + \cos (A - B),

Substitusi trigonometri

Integral yang mengandung a2 − x2

Pada integral
\int\frac{dx}{\sqrt{a^2-x^2}}
kita dapat menggunakan
x=a\sin(\theta),\quad dx=a\cos(\theta)\,d\theta, \quad \theta=\arcsin\left(\frac{x}{a}\right)
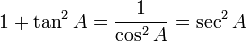
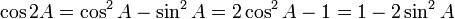
\begin{align} \int\frac{dx}{\sqrt{a^2-x^2}} & = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2-a^2\sin^2(\theta)}} = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2(1-\sin^2(\theta))}} \\[8pt] & = \int\frac{a\cos(\theta)\,d\theta}{\sqrt{a^2\cos^2(\theta)}} = \int d\theta=\theta+C=\arcsin\left(\frac{x}{a}\right)+C \end{align}
Catatan: semua langkah diatas haruslah memenuhi syarat a > 0 dan cos(θ) > 0;

Integral yang mengandung a2 + x2

Pada integral
\int\frac{dx}{{a^2+x^2}}
kita dapat menuliskan
x=a\tan(\theta),\quad dx=a\sec^2(\theta)\,d\theta
\theta=\arctan\left(\frac{x}{a}\right)
maka integralnya menjadi
\begin{align} & {} \qquad \int\frac{dx}{{a^2+x^2}} = \int\frac{a\sec^2(\theta)\,d\theta}{{a^2+a^2\tan^2(\theta)}} = \int\frac{a\sec^2(\theta)\,d\theta}{{a^2(1+\tan^2(\theta))}} \\[8pt] & {} = \int \frac{a\sec^2(\theta)\,d\theta}{{a^2\sec^2(\theta)}} = \int \frac{d\theta}{a} = \frac{\theta}{a}+C = \frac{1}{a} \arctan \left(\frac{x}{a}\right)+C \end{align}
(syarat: a ≠ 0).

Integral yang mengandung x2 − a2

Pada integral
\int\sqrt{x^2 - a^2}\,dx
dapat diselesaikan dengan substitusi:
x = a \sec(\theta),\quad dx = a \sec(\theta)\tan(\theta)\,d\theta
\theta = \arcsec\left(\frac{x}{a}\right)
\begin{align} & {} \qquad \int\sqrt{x^2 - a^2}\,dx = \int\sqrt{a^2 \sec^2(\theta) - a^2} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\ & {} = \int\sqrt{a^2 (\sec^2(\theta) - 1)} \cdot a \sec(\theta)\tan(\theta)\,d\theta = \int\sqrt{a^2 \tan^2(\theta)} \cdot a \sec(\theta)\tan(\theta)\,d\theta \\ & {} = \int a^2 \sec(\theta)\tan^2(\theta)\,d\theta = a^2 \int \sec(\theta)\ (\sec^2(\theta) - 1)\,d\theta \\ & {} = a^2 \int (\sec^3(\theta) - \sec(\theta))\,d\theta. \end{align}

Teknik pemecahan sebagian pada pengintegralan

Polinomial tingkat pertama pada penyebut

Misalkan u = ax + b, maka du = a dx akan menjadikan integral
\int {1 \over ax+b}\,dx
menjadi
\int {1 \over u}\,{du \over a}={1 \over a}\int{du\over u}={1 \over a}\ln\left|u\right|+C = {1 \over a} \ln\left|ax+b\right|+C.
Contoh lain:
Dengan pemisalan yang sama di atas, misalnya dengan integral
\int {1 \over (ax+b)^8}\,dx
akan berubah menjadi
\int {1 \over u^8}\,{du \over a}={1 \over a}\int u^{-8}\,du = {1 \over a} \cdot{u^{-7} \over(-7)}+C = {-1 \over 7au^7}+C = {-1 \over 7a(ax+b)^7}+C.

Integral Parsial

Jika dimisalkan u = f(x), v = g(x), dan diferensialnya du = f '(x) dx dan dv = g'(x) dx, maka integral parsial menyatakan bahwa:
\int f(x) g'(x)\, dx = f(x) g(x) - \int f'(x) g(x)\, dx\!
atau dapat ditulis juga:
\int u\, dv=uv-\int v\, du\!

intergal

Posted by : Unknown on :Senin, 23 September 2013 With 0komentar
| 0 komentar
Next → ← Prev
Rss: Top
▲Top▲